2024年度(令和6年度)の横浜市立南高校附属中学校の適性検査Ⅱの問題の解説をしています(適性検査Ⅰの解説はこちらへ)。
2024年度(令和6年度)の問題と解答が、カナロコ(神奈川新聞のサイト)で公表されていますので、まずは問題をダウンロードしてください。
「声の教育社」より最新年度が収録された過去問が発売されています。
適性検査Ⅱの問題構成
4つの大問での構成でした。
大問1
歯車の組み合わせに関する問題。
歯車を組み合わせる場合には、最小公倍数を利用することに気が付けるか。
スピログラフを題材にした問題です。このスピログラフで、歯車を組み合わせて花のような模様(幾何学模様)を描いて遊んだことはありました?
小さいころに遊んだおもちゃからの出題という、横浜南の得意分野でしたね。
実際に遊んだことがあると、問題を解く時にイメージがしやすかったかもしれません。
大問2
飽和水蒸気と熱伝導に関する問題。理科の分野ですが、ほぼ計算という感じでした。
前半の飽和水蒸気に関する問題は、よくある問題なのでしっかりと解けるようにしましょう。
後半の熱伝導に関しては、値が小さいほど熱を逃さない「断熱性が高い」ことになるので、その辺りの頭の変換が慣れていないとごちゃごちゃになってしまったかもしれません。
厚さが異なる場合の比較の方法については、工夫して比較することで、短時間でミスなく解けるようにしたいですね。
大問3
適正検査の王道の問題である、n進法でした。
今回は十六進法についてでした。
十六進法の場合、10以上の数値にアルファベットをあてることの意味が分かったか(事前に経験していたか)で混乱せずに取り組めたかが決まったかと思います。n進法の練習は、10より少ない数(2進法とか5進法とか)で行うことが多いので、一度でも10以上の数を経験していると強かったかも。
あとは、十六進法の考え方で繰り上げや繰り下げの計算ができれば、それほど難しくはなかったかと思います。
RGB値と十六進法の関係を理解しようと読み込むと時間が足りなかったかもしれません。
大問4
電池のしくみ、燃料電池まで含んだ内容で、理科の範囲でしたが、円グラフの読み取りや自由記載での解答など内容は満載でした。
概算での計算が素早く(手抜きして)行えるかも問われた問題でした。
電池の仕組みと水の電気分解→燃料電池のしくみ、と内容は小学生には少し背伸びした問題でしたが、身近な科学を取り上げるのは最近の横浜南の特徴でもありますね。
最後の会話文1で、先生があれっ?感じでみなみさんに質問していましたが、問題を読みながら表2の結果に疑問ってわきましたか?
自分は問題を読みながら、表2の実験結果は失敗だったのでは?と思ったのですが、先生はきちんとそこを指摘していましたね。実験するときに仮説をきちんと持つことは大切だということだと思います。
解答・解説
大問1
問題1
問題1
下線部について、ハンドルがついた歯車を【図2】の状態から時計回りに1回転した時の図を、次のア~エから1つ選び、記号を書きなさい。


問題1 解説
パンダの歯車の歯数は10個、ペンギンの歯車の歯数は8個となります。
ペンギンの歯車の「谷」の部分を10個分移動させるように回転した状態を確認します。
問題2
問題2
[ あ ][ い ]にあてはまる最も小さい整数をそれぞれ答えなさい。
【図2】の状態からハンドルを時計周りに回して、再び【図2】の状態に戻るにはハンドルがついている歯車を[ あ ]回転させればいいということですね。

3つの歯車が動いた歯数は同じになっています。つまり【図4】の状態からハンドルを時計回りに回して、再び【図4】の状態に戻るには[ い ]個分の歯数が動けばいいということですね。
問題2 解説
[ あ ]の解説
歯数が10個の歯車(パンダ歯車)と歯数が8個の歯車(ペンギン歯車)の組み合わせの場合は、2つの歯数の最小公倍数ごとに回し始めの状態になる。
10と8の最小公倍数は40なので、歯数が40動くごとに回し始めとなる。
ハンドルのついたパンダ歯車は歯数が10個なので、40歯数動くのには4回転必要となる。
[ い ]の解説
歯数が8個、10個、15個の3つの歯車の場合は、3つの数字の最小公倍数を求めればよいので、120個分の歯数を動かせばよい。
問題3
問題 3
みなみさんは、次の条件で模様を描きました。条件1で描いた模様と、条件2で描いた模様として最も適切なものを、次のア~カから1つずつ選び、それぞれ記号を書きなさい。
条件1:AのわくとBの歯車を使って、模様を描く。
条件2:AのわくとDの歯車を使って、模様を描く。

問題3 解説
【写真2】~【写真5】の例は、AとC(歯数40の歯車)の組み合わせとなるので、ここでAとCについて考えてみる。
問題2より、ふたつの歯車の歯数の最小公倍数となった時に、スタートした状態に戻る。これは花びらの模様の線が閉じることを表している。
96と40の最小公倍数は480となるので、480の歯数を動いたら歯車Cはスタートした状態に戻ることとなる。
歯車Cは、480÷40=12周で元に戻る。
Cの花びらの数は12とあるので、内側の小さな歯車の回った数が花びらの数と等しい。
【条件1】Aと歯車B(歯数60)
96と60の最小公倍数は480となるので、歯車Bは、480÷60=8周でもとにもどるので、花びらの数が8である模様が答えとなるので、『ウ』が該当する。
【条件2】Aと歯車D(歯数30)
96と30の最小公倍数は480となるので、歯車Dは、480÷30=16周でもとにもどるので、花びらの数が16である模様が答えとなるので、『カ』が該当する。
問題4
問題 4
みなみさんは模様を描いていくうちに、円形のわくと歯車の組み合わせによって花びらの数が変化していることに気づき、花びらの数の求め方を言葉の式で次のように考えました。[う]、[え]にあてはまる言葉を答えなさい。
ただし、「わくの歯数」と「歯車の歯数」という言葉を使うこと。同じ言葉は何回使ってもよいものとする。
花びらの数 = [う]÷[え]
問題4 解説
問題3の解説を参考のこと
別解として、[わくの歯数]÷[わくの歯数と歯車の歯数の最大公約数]でも成り立つ
大問2
問題1
問題 1
【会話文1】をもとに「ペットボトルのまわりに水滴がつく理由」や「冬に吐く息が白くなる理由」などについて、次のようにまとめました。①~③にあてはまる言葉を、次のア、イから1つずつ選び、それぞれ記号を書きなさい。
「ペットボトルのまわりに水滴がつく理由」は、ペットボトルの中の冷たい液体によって、ペットボトルのまわりの空気が( ① )、ペットボトルのまわりの空気にふくむことのできる水蒸気の量が( ② )ためである。また、「冬に吐く息が白くなる理由」は、息にふくまれていた水蒸気が、まわりの( ③ )空気に触れて水滴となったためである。
① ア あたためられて イ 冷やされて
② ア 減った イ 増えた
③ ア あたたかい イ 冷たい
問題1 解説
温度が冷えることで、空気中に含むことができる水蒸気の量が減り、水蒸気が水滴として現れることによる。
問題2
問題 2
[ あ ][ い ]にあてはまる数をそれぞれ答えなさい。[ い ]については、小数第一位を四捨五入して、整数で答えなさい。
(みなみさん)この教室の気温は20℃で、体積は170m3なので、最大で[ あ ]gの水蒸気をふくむことができるのですね。
(先 生)その通りです。ちなみに、みなみさんが今もとめたものは、湿度が100%であったときの水蒸気の量です。今、この教室の湿度は65%です。
(みなみさん)ということは、今、この教室の空気中にふくまれている水蒸気の量は[ い ]gとなりますね。
問題2 解説
[ あ ]は、体積170m3の教室に含むことができる最大の水蒸気量を求める。
気温と空気の体積によって含むことができる水蒸気の量が異なってくる。
気温が20℃で、体積が1m3の空気は、最大で17.3gの水蒸気を含むことができるので、170m3の体積の空気には
170 × 17.3 = 2941
となるので、[ あ ]は2941となる。
[ い ]は、湿度が65%なので、[ あ ]で求めた最大量2941gの65%を求めればよいので、
2941 × 0.65 = 1911.65
であるので、小数点第一位を四捨五入して、1912となる。
問題3
問題 3
【会話文3】と【資料1】からいえることとして適切なものを、次のア~エからすべて選び、記号を書きなさい。

ア 断熱材は、室外の気温を室内に伝わりにくくするためのものである。
イ 結露を防ぐためには、換気を十分にして、室内の水蒸気の量を増やしていくことが大切である。
ウ フェノールフォームとセルロースファイバーは、同じ厚さであった場合には、セルロースファイバーの方が断熱性は高くなる。
エ ビーズ法ポリスチレンフォームは、水に強い性質がある。
問題3 解説
ア・・・【会話文3】中の前半で、先生が「断熱材を使用して、室外の気温を室内に伝わりにくくする工夫が考えられます。」と言っているので、正しい。
イ・・・【会話文3】中の後半で、先生が「換気扇を回すなど、水蒸気を外へ逃がすことにより、結露を防ぐことができます。」と言っているので、室内の水蒸気量を減らすことが結露の防止につながるので、誤り。
ウ・・・【資料1】の下に、同じ「厚さ」であれば「熱伝導率」が小さいほど、断熱性が高くなる、とある。【資料1】よりフェノールフォームの熱伝導率は0.019、セルロースファイバーは0.039と分かるので、熱伝導率の数値が小さいフェノールフォームのほうが断熱性が高いので、誤り。
エ・・・【資料1】よりビーズ法ポリスチレンフォームは耐水性があることが分かる。「耐水性」とは、【資料1】の下によると水にぬれても水分がしみ通らないなど、水に強い性質。とあるので、正しい。
問題4
問題 4
【資料1】の断熱材A~Dの厚さが、Aが0.05m、Bが0.015m、Cが0.025m、Dが0.1mであったとき、断熱材A~Dの断熱性の高さはどのようになりますか。断熱性が高い順番に、A~Dを並びかえてその順番を答えなさい。
問題4 解説
【資料1】の下の説明より、
同じ「厚さ」であれば、「熱伝導率」が小さいほど、断熱性が高くなる。
同じ「熱伝導率」であれば、厚みがあるほど、断熱性が高くなる。
したがって「厚さ÷熱伝導率」の値によって、断熱性の高さを表すことができる。
よって、「厚さ÷熱伝導率」を求めて、高い順に並べれば断熱性が高い順となることが分かる。
A・・・0.05 ÷ 0.038
B・・・0.015 ÷ 0.019
C・・・0.025 ÷ 0.034
D・・・0.1 ÷ 0.039
計算の結果、
Aは、1.315…
Bは、0.789…
Cは、、0.735…
Dは、2.56…
となるので、D → A → B → C。

値を求めよではなく、大小関係が分かればよいので、すべてを計算する必要はないよね?
どうすればよいのかしら

割り算どうしをくらべるには、「割られる数(÷の左側)」か「割る数(÷の右側)」のどちらかを同じ(概算で計算するならほぼ同じでもよい)にして考えてみましょう。
「割られる数」が同じであれば、「割る数」が小さいほうが計算結果は大きくなりますね。 △÷2 のほうが △÷3 よりも大きくなる。
「割る数」が同じであれば、「割られる数」が大きいほうが計算結果は大きくなりますね。 10÷ ◇ のほうが 5 ÷ ◇ よりも大きくなる。
AとDを比べてみると、「割る数」がほぼ同じ(0.038と0.039)なので、「割られる数」が大きい(0.1と0.05は明らかに大きさが違う)方が、結果が大きくなるので、D > Aとわかる。
次に、AとBを比べてみる。Aの「割る数」0.038はBの「割る数」0.019の2倍であるので、「割る数」をそろえてみて大小を確認する。
ここでは、Bの「割る数」を0.038に合わせてみる(「割られる数」と「割る数」を両方とも2倍する)
A ・・・0.05 ÷ 0.038
B’・・・0.03 ÷ 0.038
となるので、「割られる数」が大きいAのほうが計算結果は大きくなるので、A > Bと分かる。
先ほどの結果と合わせて、D > A > Bという大小関係であることが分かった。
のこりは、Cがどこに入るのかを探してみる。
ざっと見ると、AとCは「割られる数」を簡単に合わせやすそうなので、AとCを比較してみる。
C‘・・・0.05 ÷ 0.068 とできるので、「割る数」の大きいC’のほうが小さいことが分かるので、A > C。
よって、CとBの大小を比較すれば、4つの大きさの順番が分かる。
BとCの「割られる数」を同じにして、比較してみる。例えば、「割られる数」を0.075にそろえて比較する。
B‘’・・・0.075 ÷ (0.019 × 5)
C‘'・・・0.075 ÷ (0.034 × 3)
C‘’の「割る数」が大きくなる(ざっくりと100は超えそう、一方B’’は100は超えない)ので、C’’がB’’よりも小さくなることが分かる。
これで、D > A > B > C ということが分かった。
この問題は、値を求めるのではなく大小関係が分かればよいので、ひっ算でがむしゃらに割り算する前に、計算しない(もしくは簡単な概算)で答えがでる方法はないかと、まず立ち止まって日ごろから考えることはとても大事です。
厚さ(「割られる数」)が5の倍数の綺麗な数字。
熱伝導率(「割る数」)が、AはBの2倍の数、AとDはほぼ同じであることに気づければ、割り算の式を作っただけで計算をせずに大小が判断できると、気づけるようにしたいですね。
大問3
問題1
問題 1
十進法の考え方、しくみとして正しいものを、次のア~エからすべて選び、記号を書きなさい。
ア 999の次の数は、1つ上の位の数を1にして、他の位の数を0にする。
イ 最初の数は0であり、100番目の数は100である。
ウ 一番大きなくらいの数が9より大きくなったら、位が1つ上がる。例えば、123の場合は、一番大きな位の数が9より大きくなったら、位が1つ上がり1023になる。
エ 一の位、十の位、百の位、…のように、位が1つ上がるごとに1つ上の位は10倍になっている。
問題1 解説
ア 999の次の数は、1つ上の位の数を1にして、他の位の数を0にする。
→ 999の次の数は1000となるので、正しい
イ 最初の数は0であり、100番目の数は100である。
→ 最初の数は0であるが、100番目の数は99となるため、誤り。
ウ 一番大きなくらいの数が9より大きくなったら、位が1つ上がる。例えば、123の場合は、一番大きな位の数が9より大きくなったら、位が1つ上がり1023になる。
→ 少しわかりにくいですが、123の百の位を一つずつ大きくして、123、223、323、…923とすると、次に百の位が1つ大きくなったらどうなるのかが問われているので、1023になるで正しい。
エ 一の位、十の位、百の位、…のように、位が1つ上がるごとに1つ上の位は10倍になっている。
→ n進法は、位が1つ上がるたびに位がn倍になっているので、正しい。
問題2
問題 2
[ ★ ]にあてはまる数を漢数字で答えなさい。
【会話文2】中のみなみさんが「十六の位の1つ上の位は、[ ★ ]の位ということでしょうか。」
問題2 解答
問題2 解説
十進法では、一の位、十の位、百の位、千の位、…となる。
十六進法では、一の位、十六の位、[ ★ ]の位、となるのでその位がいくつになるかを答えなさい、ということ。
| 1つ目の位 | 2つ目の位 | 3つ目の位 | 4つ目の位 | |
|---|---|---|---|---|
| 十進法 | 一の位 | 十の位 = 10 | 百の位 = 10×10 | 千の位 = 10×10×10 |
| n進法(一般的なルール) | 一の位 | nの位 | n × n の位 | n × n × nの位 |
| 十六進法 | 一の位 | 十六の位 = 16 | [ ★ ]の位 |
位とn進法の関係は上の表のとおりとなる。
十進法で、位について確認しながら、n進法(一般的なルール)を見つけていくと
1番目(1番小さな)位は、一の位である。これは、何進法であっても一の位となります。
2番目の位は、十の位となります。これは、十進法の十と同じ数となります。よって、n進法ならnの位となります。
3番目の位は、百の位となります。これは、10×10ということです。n進法なら n × n の位となります。
4番目の位は、千の位となります。これは、10×10×10ということです。n進法なら n × n × n の位となります。
よってn進法と位の一般的なルールはこうです。「△番目の位は、n進法の n の数字を (△ - 1)回かけた数字」となります。
十進法の4番目の位で確認してみると、10を(4-1)回かけた数値、すなわち10×10×10=1000で、千の位ということになります。
[ ★ ]の位は、十六進法の3つ目の位ということなので、16を2回かけた数となるので16×16=256となります。
漢数字で表すと二百五十六です。
問題3
問題 3
カラーコード#6C2735 をRGB値( , , )で表しなさい。
問題3 解説
カラーコードは、十六進数の二桁の数字が、3つ連続してできている。
6桁の数字で表現されているが、6桁ではなく(十六進数で表記された)2桁の数が3つ横に並んだものということである。

RGBコードは、その3つの十六進数を十進数で表して、カンマで区切って表示する。
よって、16進数で表現された「6C」「27」「35」を10進数ではどのような数字になるかを求める。
【会話文2】の【表1】の下の2回目のみなみさんの発言
「だんだんとわかってきました。次に、16進数から10進数への変換について考えたいです。例えば、16進数で表された54は、10進数に変換すると、16×5+1×4=84となり、10進数では84を表しているということですか。」
この考え方を利用して、「6C」「27」「35」を10進数に変換していきます。
「6C」=16×6+1× C
ここで、【表1】より16進数の C は、10進数の12であることが分かるので、「6C」を改めて変換すると
「6C」=16×6+1×12=96+12=108
「27」=16×2+1×7=32+7=39
「35」=16×3+1×5=48+5=53
問題4
問題4
下線部のように、みなみさんは、#A589C7の補色のカラーコードを、16進数を使って次のように求めました。次の(1)(2)に答えなさい。
#A589C7の補色のカラーコードを、16進数を使って求めます。
最大値は[ あ ]、最小値は[ い ]だから、合計値は[ う ]
補色のカラーコードは、
赤(R)の値は、[ う ]ー A5
緑(G)の値は、[ う ]ー 89
青(B)の値は、[ う ]ー C7
よって、補色のカラーコードは、#[ え ]になります。
(1)[ あ ]、[ い ]、[ う ]にあてはまる値を、16進数でそれぞれ答えなさい。
(2)[ え ]にあてはまるカラーコードを答えなさい。
問題4 解説
まず、カラーコード#A589C7から、最大値と最小値を求めます。
(1)では、十六進数で答えるように指示があるので、10進数に変換しないで大小を比較します。
「A5」「89」「C7」の大小を比較する。
最大値は十六の位(2つ目の位)が最も大きいものを選べばよいので、C >A >8より、最大値は「C7」
最小値は十六の位(2つ目の位)が最も小さいものを選べばよいので、C >A >8より、最小値は「89」
合計は16進数のまま、C7+89を計算してみる。
一の位どうしの足し算は、7+9=16となる。16進数とは16になったら次の1つ上の位に1つ上がるということ。
C7+89の答えの一の位は0だということが分かる。
そして、2つ目の位(十六の位)に1の繰り上げがあったことなので、次に2つ目の位(十六の位)を計算する。
C +8+1(←繰り上げ分)
<16進数のまま計算>
【表1】をみると、Cはあと3つ(D、E、F)に+1で繰り上がる、すなわち+4で繰り上がることになる。よって、(8+1)から4を引いた数(9-4=5)が2つ目の位(十六の位)に残る。3つ目の位(二百五十六の位)が1、2つ目の位(十六の位)が5となる。
<10進数に変換して計算>
C+8+1の計算だけ、一度10進数に変換して計算したのちに16進数にもどすと、Cは【表1】より10進数では12なので、
12+8+1=21(10)となる。
21(10)を16進数に変換する場合は、21=16 × △ +1 × ◇ となる△と◇を求めればよいので、△は1、◇は5となる。
※数字(n) という表記は、この数字はn進数であることを示す。
どちらで求めても、最大値+最小値の合計値は16進数で150となる。
(2)で#A589C7の補色のカラーコードを求めます。
ここでも、できるだけ16進数で話をすすめます。
赤の場合、150 ー A5となります。
一の位どうしの引き算を考えます。0-5で引き算ができないので一つ上の位から1を借りて引き算するところは、通常の10進数と同じです。
ただし、上の位から1を借りることは、16進数では10ではなく16となります。
よって、16-5=11となりますが、【表1】より11は16進数ではBと表すので、1の位はBとなります。
次に2つ目の位(十六の位)の引き算を考えます。
先ほどの一の位の引き算で、150は二つ目の位から1を貸しているので、4 - A となります。Aは4よりも大きいのでふたたび次の位から1を借りることになります。よって、4ではなく、16+4=20とAの引き算となります。
20ーAとなりますが、16進数では計算しにくいので10進数で考えて16進数に戻すことにします。
【表1】よりAは10なので、20-10=10となります。再び【表1】より10は16進数ではAとなります。
150 ー A5の結果を16進数で表すと「AB」となります。
緑の場合、150 ー 89となります。
同様に一の位は、16ー9=7
2つ目の位(十六の位)は、20-8=12となるので、【表1】より12は16進数ではCとなります。
よって、150 ー 89=C7
青の場合、150 ー C7となります。
同様に一の位は、16ー7=9
2つ目の位(十六の位)は、20-C=20-12=8となります。
よって、150 ー C7=89
補色のカラーコードは、#ABC789 となります。
大問4
問題1
問題1
①__について、ガソリンなどの燃料を燃やしたときに、地球温暖化の原因の1つとされる二酸化炭素が発生します。二酸化炭素が存在するかどうかを確かめるための実験方法とその結果を述べた次の文の[ あ ]、[ い ]にあてはまる言葉を答えなさい。
燃料を燃やした時に発生した気体が入った試験管に[ あ ]を入れてふると、[ あ ]が[ い ]。このことから二酸化炭素が存在することがわかる。
問題1 解説
二酸化炭素の確認をする有名な方法ですね。教科書レベルの内容なのでこの程度は書けるようにしておきましょう。
問題2
問題2
②__について、次のグラフは2010年度、2021年度の1年間の日本の発電量について発電方法ごとの割合を示したものです。

このグラフについて述べた文章として適切なものを、次のア~エから1つ選び、記号を書きなさい。
ア 2021年度には、2010年度よりも発電量の合計が増えている。
イ 2021年度の水力発電による発電量は、2010年度の水力発電による発電量よりも大きい。
ウ 2021年度は、「石炭」、「天然ガス」、「石油等」による発電以外の発電方法の割合が全体の4分の1をこえている。
エ 2021年度の太陽光、風力、地熱、バイオマスによる発電量の合計は1000億KWhより少ない。
問題2 解説
ア 発電量の合計は、2010年度が11,494億kWh、2021年度は10,328億kWhと減っている。誤り。
イ 水力発電の占める割合は、2010年度の7.3%から2021年度は7.5%と増えている。ただし、アでみたように全体の発電量は2021年度のほうが減っている。発電量を計算するには、発電量の合計×割合を計算して比べるべきであるが、割合が0.2%増えているが、発電量の合計が2021年度は2010年度に比べて10%減っているので、水力発電による発電量は減っている。
実際に計算して比べてみると、2010年度の水力発電の発電量は、11,494億kWh×7.3%=約839億kWh。2021年度は、10,328億kWh×7.5%=約774億kWhとなる。
ウ 2021年度の「石炭」、「天然ガス」、「石油等」による発電方法の割合の合計が75%よりも小さければよい。
3つの発電方法の割合の合計は、31.0% + 34.4% + 7.4% = 72.8%と75%よりも小さいので、正しい。
エ 2021年度の発電量で1000億kWhとなるには、割合として10%程度となる。太陽光、風力、地熱、バイオマスの発電方法の割合の合計が10%よりも少なければよい。発電割合の合計は、8.3% + 0.9% +0.3% + 3.2%となり10%は超える割合となるので、4つの発電量の合計は 1000億kWhよりも大きくなるので、誤り。
問題3
問題3
実験2 アルミホイルの幅を変えて、発生する電流の大きさを調べる。
【図2】は実験2の装置です。

実験2の[ ]にあてはまる仮説として適切なものを、次のア~エから1つ選び、記号を書きなさい。
ア ティッシュペーパーと接するアルミホイルの面積が大きいほど、発生する電流は大きくなるのではないか。
イ 木炭とティッシュペーパーとアルミホイルでつくった装置の数が多いほど、発生する電流は大きくなるのではないか。
ウ ティッシュペーパーと接するアルミホイルの枚数が多いほど、発生する電流は大きくなるのではないか。
エ アルミホイルを木炭にまく回数が多いほど、発生する電流は大きくなるのではないか。
問題3 解説
ア アルミホイルの幅が変わると、ティッシュペーパーとアルミホイルの接する面積が変わる。このことから、ティッシュペーパーと接するアルミホイルの面積が大きいほど、発生する電流の大きくなるかを調べる仮説としては、正しい。
イ アルミホイルの幅を変えても、装置自体の数は増えないので、イの仮説は不適切である。
ウ ティッシュペーパーに接するアルミホイルの幅を変えるだけで、枚数は変えないので、ウの仮説は不適切である。
エ 実験2はアルミホイルを木炭にまくわけではないので、エの仮説は不適切である。
問題4
次の【会話文1】は、実験4の実験方法について先生とみなみさんが会話した内容です。[ う ]にあてはまるものとして、適切な言葉を答えなさい。
実験3および実験4では【図3】の装置を使用している。
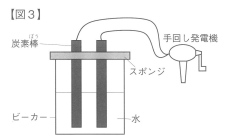
【会話文1】
先生:実験4の方法について、もう少しくわしく教えてほしいのですが、炭素棒はスポンジで固定して動かさずに、水かさだけを変化させて、水の量と発生する電流の大きさの関係を調べたのでしょうか。
みなみさん:はい、そうです。
先生:水かさが増えることによって変化したのは、水の量だけですか。
みなみさん:水の量だけでなく[ う ]も増えています。
先生:そうですね。[ う ]は変えずに、水の量だけを変える方法を考えてもう一度実験してみましょう。
問題4 解説
先生の突っ込みはさすがですね。
先生の頭の中では、水の量を単純に増やしたとしても発生する電流の大きさは変わらないはず、という仮説があったようです。
水の量を増やした場合に変わりそうなのは、電流の大きさではなく、発生し続ける時間、とかではないでしょうか?
発生する電流の大きさが変わりそうな候補としては、濃度とか、装置の大きさとか、・・・
水に水を加えても濃度は変わらないですよね。
装置の一部を長くする、太くする・・・こういったことで、発生する電流の大きさが変化したのでは?と思ってみると、水を加えることで炭素棒が水につかる部分が増えることになりますね。
水の量を増やしても、炭素棒に触れる水の面積が一定になるような実験のやり方は思いつきました?
一般的な理科の実験室や身近なものでできないか、考えてみるのも面白いかもしれませんね。
まとめ
大問4つの構成は、令和5年度と同じでした。
まずは確実に解ける問題はミスなく解くことが大事です。
そして、一筋縄でいかない問題に取り組む時間を確保するためには、確実に解ける問題はなるべく短い時間で、ミスしない手続きで解くことが必要になってきます。
今回もかつての横浜南のように捨て問はなかったと思います。
時間内にすべてを解くためには、ある程度このやり方で正しいと思い切る勇気も必要ですね。
横浜市立南高校附属中学の適性検査の解説のまとめ
令和5年度(2023年度)入学者向け




